Hackathon

Hosted by Deloitte \(\vert\) Berlin, Germany

The Quantum Climate Challenge 2022 posed an interesting question: Can quantum computing help reduce the climate impact of aviation? The goal was to explore how quantum algorithms can be used to optimize flight trajectories in a way that minimizes the contribution of air travel to anthropogenic climate change, while still complying with strict air traffic regulations.

The Problem: Climate-Optimized Air Traffic

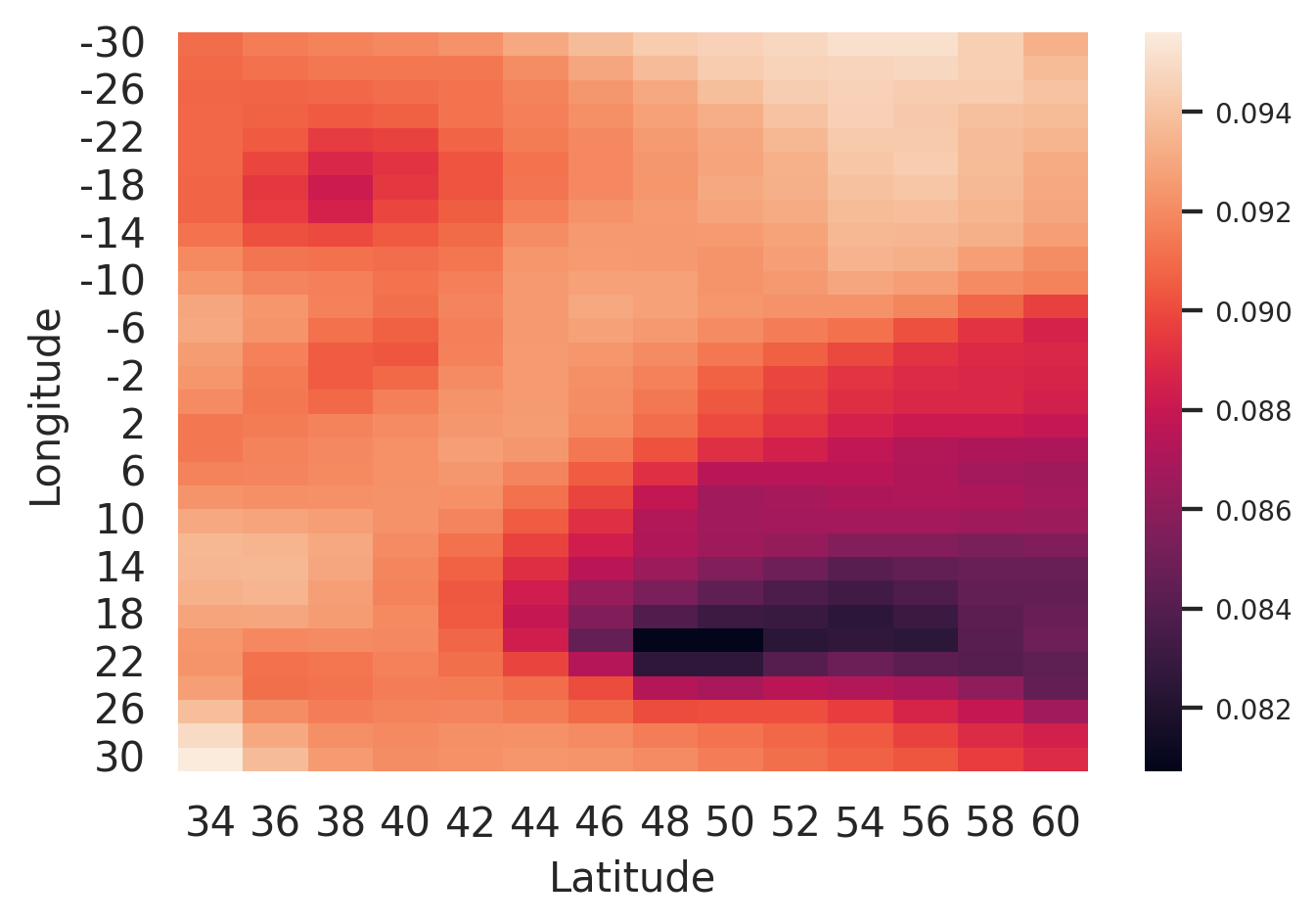
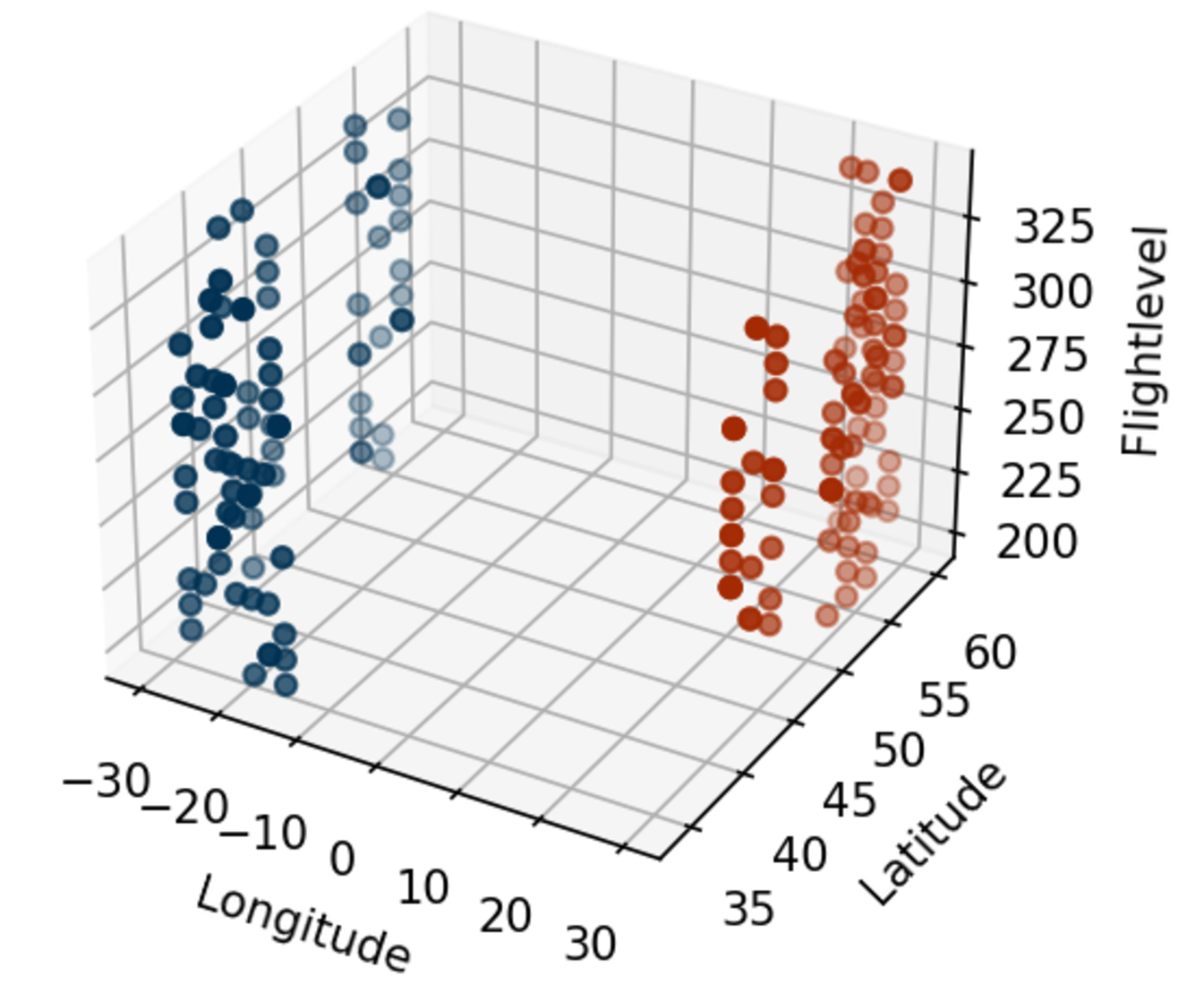
At its core, the challenge was a constrained combinatorial optimization problem. Given \(99\) flights traversing European airspace, the task was to determine flight paths that minimize the net climate impact, quantified by a modeled temperature increase \(\Delta T\). This impact depends on multiple factors—fuel burn, contrail formation, \(NOx\) emissions, altitude, timing, and even weather conditions—captured in a high-resolution \(4D\) climate model based on ERA5 data and algorithmic Climate Change Functions (aCCFs).

The optimization landscape was further complicated by real-world aviation constraints:

• Aircraft physics and aerodynamics (e.g., stall speed, turn radius)
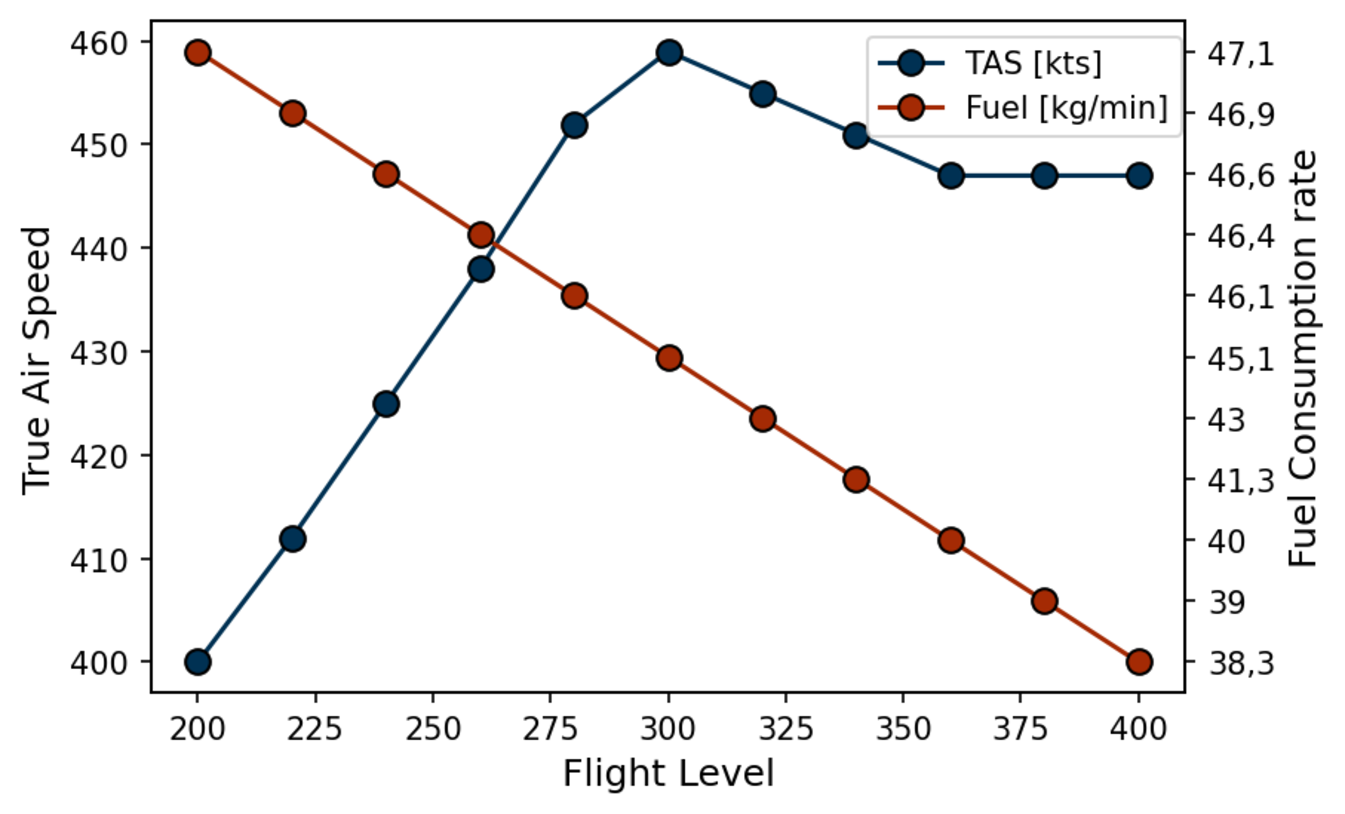
• Fuel consumption at varying altitudes
• Regulatory safety separations (5 NM horizontal, 1000 ft vertical)
• Air traffic management protocols (DFS Germany standards)

To make this problem suitable for NISQ-era quantum devices, I decomposed it into two subproblems:

• Climate Trajectory Optimization: Find routes that minimize the climate impact.
• Conflict Resolution: Adjust trajectories to avoid collisions, while preserving minimal climate cost.

Problem Decomposition & Quantum Approach

Trajectory Optimization

I casted this a discrete pathfinding task across a 3D voxel grid (latitude, longitude, altitude) with time discretized in three 6-hour intervals. Each trajectory’s cost was defined by the climate impact (\(\Delta C \cdot\) fuel), and the challenge was to find low-cost paths through the grid. My classical baselines used Dijkstra’s algorithm with climate-weighted graphs.

Conflict Resolution

After generating initial paths, overlapping trajectories were inevitable. The resolution step involved selecting altitude shifts (\(\pm 20\) FL) to deconflict flights. This task was framed as a QUBO problem, making it amenable to quantum optimization. The binary vector \(\Delta z \in \{0,1\}^N\) encoded detour decisions, and the cost function \(Q(\Delta z)\) accounted for both climate penalty and safety constraints.

My Approach: Filtering VQEs

I implemented two quantum algorithms to solve the problem, with most of my effort and insight focused on the Filtering Variational Quantum Eigensolver, which is discussed in the accompanying Github repository.

Results

The fight path finding algorithm provided reasonable results, with scalability limited by pre-sampling and qubit count. F-VQE stood out by effectively resolving conflicts without introducing new ones, demonstrating the method’s power in structured QUBO optimization.

With this project, I was able to secure the \(2^\text{nd}\) place out of over \(130\) participating teams.